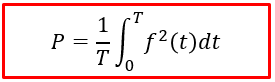Náplň prednášky:
- Fourierov rad - Komplexný tvar
- Komplexné, modulové a argumentové spektrum periodického signálu
- Výkonové spektrum a Parcevalova teorema
Fourierov rad – Komplexný tvar
- Okrem trigonometrického a kosínusového tvaru poznáme aj komplexný (exponenciálny tvar) FR.
- S komplexným tvarom FR sa v praxi stretávame najčastejšie
- Pri komplexnom tvare nepoužívame priamo funkcie sin(t) a cos(t), ale využívame množinu exponenciálnych komplexných funkcií {ejkΩ1t }, ktorá je pre pre N =±1, ±2, … ortogonálna v intervale jednej periódy t∈ <0, T>
- Komplexné koeficienty sú určené nasledovne:
- Tieto koeficienty sú komplexné čísla a zadávajú sa v nasledovnom tvare. Koeficienty ak, bk sú zhodné s koeficientami z trigonometrického tvaru.
Komplexné, modulové a argumentové spektrum
- Je zrejmé, že komplexné spektrum nie je jednoduché zakresliť do grafu (podobne ako trigonometrický tvar). Preto sa zakresľuje modulové spektrum, ktoré predstavuje veľkosť jednotlivých spektrálnych čiar a tiež argumentové spektrum, ktoré predstavuje fázu.
Pre modulové a argumentové spektrum platí nasledovné:
- Pri modulovom a argumentovom spektre sa spektrálne čiary vyskytujú v kladnej časti aj zápornej časti horizontálnej osi v k-násobkoch základnej kruhovej frekvencie Ω1.
- Modulové spektrum je obojstranné (dvojstranné) spektrum! (t.j. kreslí sa do kladnej aj zápornej časti frekvenčnej osi).
- Argumentové spektrum vždy vykazuje nepárnu symetriu!
- Jednosmerná zložka má nulovú fázu, ale môže mať fázu +π v prípade ak by bola jednosmerná zložka záporná.
Výkonové spektrum
- Stredný normovaný výkon je P[W] je v časovej oblasti daný vzťahom:
- Výkon v spektrálnej oblasti možné určiť, ako sumu výkonov jednotlivých spektrálnych zložiek.
Parcevalová teoréma hovorí, že výkon periodického signálu v časovej oblasti je rovný jeho výkonu vo frekvenčnej oblasti!
Praktická šírka ftrekv. spektra
- Pod pojmom praktická šírka spektra periodického signálu rozumieme frekvenčný rozsah B, v ktorom sa nachádzajú frekvenčné zložky s amplitúdami prevyšujúcimi vopred stanovenú hodnotu (prah).
- Tiež pod týmto pojmom môžeme rozumieť frekvenčný rozsah, v ktorom je sústredená podstatná časť normovaného výkonu periodického signálu.
- V praxi nemá zmysel pracovať s nekonečným spektrom signálu, zvyčajne sa spektrum obmedzí na praktickú šírku.
- Spektrum signálu obmedzujeme v spektrálnej oblasti, kedy sa stanoví prah a všetky zložky pod prahom sa vynulujú.
- Tiež je možné spektrum obmedziť pomocou filtrácie (ukážeme na neskorších prednáškach)
Vplyv posunutia signálu v čase na frekvenčné spektrum
- Posunutie signálu v čase nemá žiaden vplyv na modulové (alebo aj amplitúdové) spektrum.
- Mení sa len fáza jednotlivých harmonických!