Zoradenie 1R poľa
V programovaní sa veľmi často stretávame s potrebou usporiadnania / zoradzovania prvkov. Môže ísť o prvky ako sú čísla, písmena alebo komplexné údajové štruktúry. Existuje množstvo metód a algoritmov. Na tomto predmete si ukážeme najzákladnejší algoritmus bublinkového triedenia a bežne využívaný algoritmus quck sort.
Bublinkové triedenie - bubble sort
Pracuje opakovaným prechodom cez zoznam, ktorý má byť utriedený porovnávajúc vždy dva prvky. Ak prvky nie sú v správnom poradí, zamení ich. Porovnávanie prvkov v zozname trvá, pokiaľ sú potrebné výmeny, teda pokiaľ nie je zoznam usporiadaný. Algoritmus dostal názov vďaka tomu, že menšie prvky sa „prebublinkujú“ na začiatok zoznamu.
void bubble_sort(int numbers[], const int size)
{
for(int j = size-1; j > 0; j--)
for(int i = 0; i < j; i++)
{
if(numbers[i+1] < numbers[i])
{
int tmp = numbers[i+1];
numbers[i+1] = numbers[i];
numbers[i] = tmp;
}
}
} |
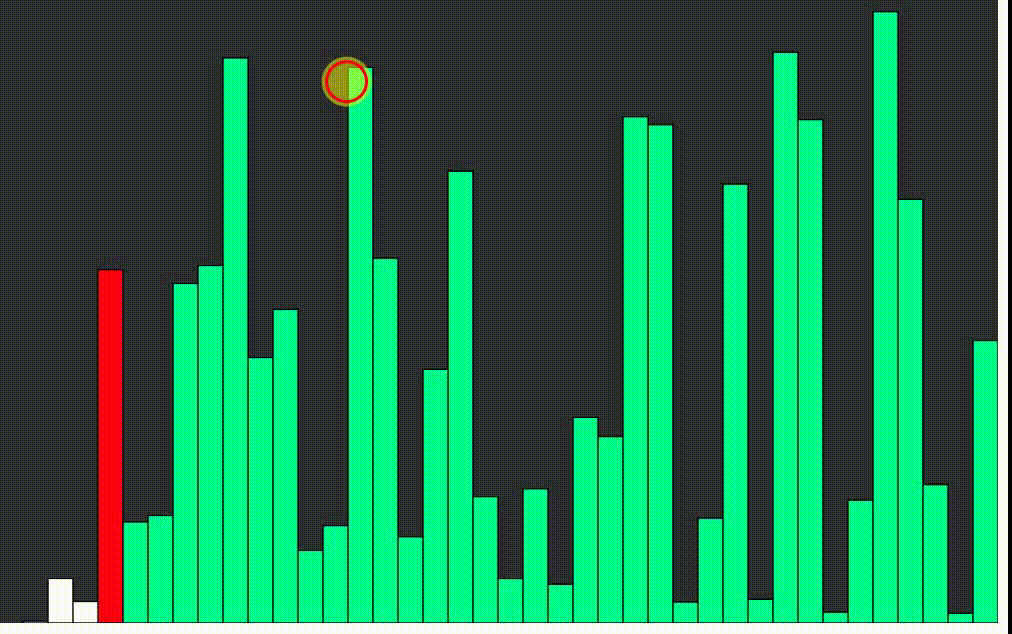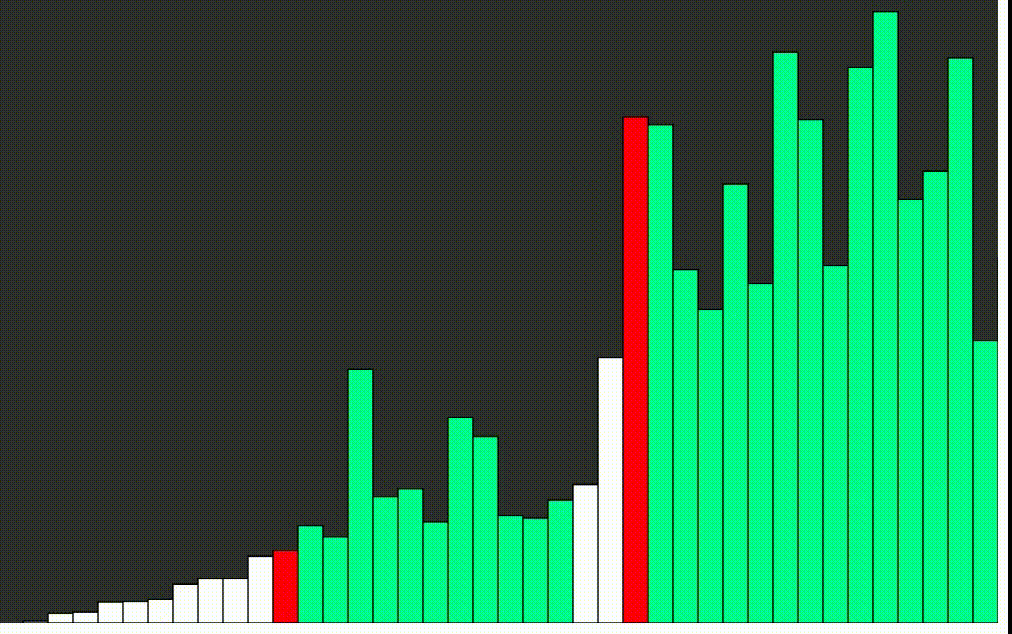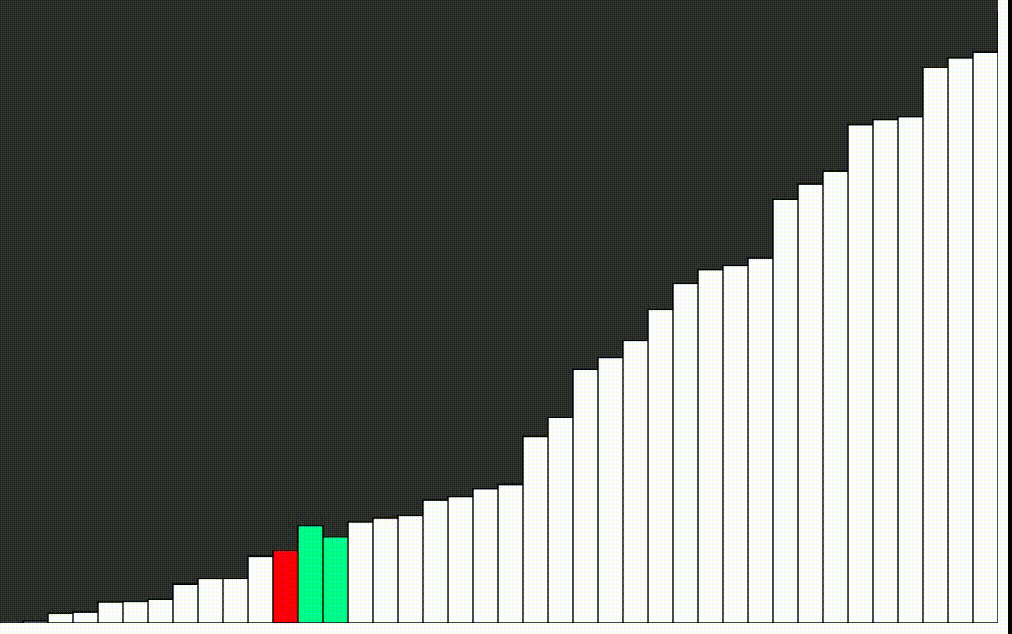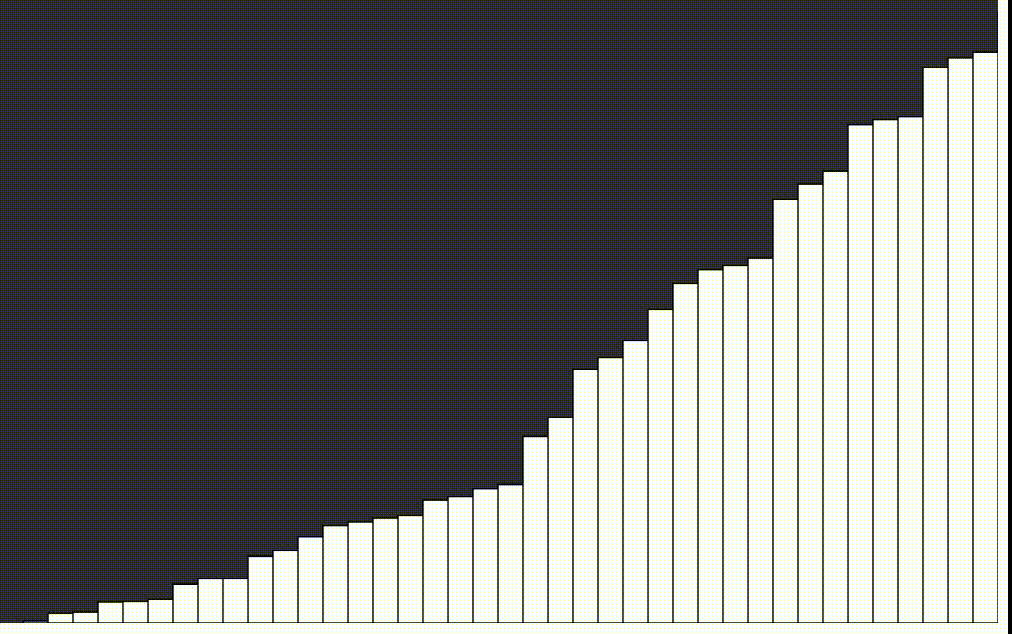
Rýchle triedenie - quick sort
Quicksort alebo rýchle triedenie je jeden z najrýchlejších známych triediacich algoritmov založených na porovnávaní prvkov. Jeho priemerná doba výpočtu je najlepšia zo všetkých podobných algoritmov. Algoritmus je aj veľmi jednoduchý. Nevýhodou je, že pri výnimočne nevhodnom tvare vstupných dát môže byť časová a pamäťová náročnosť. Algoritmus vymyslel v roku 1962 Sir Charles Antony Richard Hoare.
Základnou myšlienkou quicksortu je rozdelenie triedenej postupnosti čísel na dve približne rovnaké časti. V jednej časti sú čísla väčšie a v druhej menšie ako istá zvolená hodnota, ktorá sa nazýva pivot. Ak je táto hodnota zvolená dobre, sú obe časti približne rovnako veľké. Ak budú obe časti samostatne roztriedené, je roztriedené i celé pole. Obe časti sa potom rekurzívne triedia rovnakým spôsobom.
Pre použitie funkcie qsort() je potrebné použiť hlavičkový súbor stdlib.h. Tiež je potrebné vytvoriť porovnávaciu funkciu, ktorou qsort bude porovnávať prvky poľa.
#include <stdlib.h>
int main()
{
int pole[] = {1, 4, 2, 5, 8, 7, 3, 6};
int pocet=sizeof(pole)/sizeof(int);
qsort(pole, pocet, sizeof(int), porovnaj);
}
int porovnaj(const void* var1, const void* var2)
{
return *(int*)var1 - *(int*)var2;
}
|
Vyhľadávanie v 1R poliach
Operácia vyhľadávania patrí k najčastejším operáciám, ktoré budete nad údajmi v poli robiť. Napr. aj najdôležitejšia operácia pri práci s SQL databázami je práve operácia selekcie (vyhľadávania). V čom spočíva problém? - Máme pole, ktoré obsahuje obrovské množstvo údajov a našou úlohou je nájsť požadovaný údaj čo najrýchlejšie (a teda - čo najefektívnejšie). Rovnako ako pre zoradenie aj pre vyhľadávanie existuje mnoho algoritmov. Najzakladanejším je lineárne vyhľadávanie a pokročilejším zasa binárne vyhľadávanie.
Lineárne vyhľadávanie
Z algoritmického pohľadu je tento spôsob najjednoduchší, pretože je veľmi intuitývny. Spočíva v postupnom prehľadávaní celého poľa. Toto prehľadávanie končí ak sa dosiahne koniec poľa alebo ak sa nájde vyhľadávaný prvok.
Na vyhľadanie prvku potrebujeme minimálne jedno testovanie (to je v prípade, že hľadaný prvok je prvým prvkom poľa) O(1). V najhoršom prípade je potrebné vykonať toľko testovaní koľko je prvkov poľa O(N).
Binárne vyhľadávanie
V porovnaní s lineárnym vyhľadávaním ide o sofistikovanejší spôsob vyhľadávania. Princíp spočíva v delení intervalu (celého poľa) na subintervaly. Pritom sa hľadaný prvok porovnáva s prostredným prvkom daného subintervalu. Ak nie sú zhodné vyhodnotí sa, či je hľadaný prvok väčší alebo menší a vyhľadávanie sa zúži na oblasť vľavo alebo vpravo od prostredného prvku. Takto sa vždy eliminuje polovica prvkov poľa.
Na vyhľadanie prvku potrebujeme minimálne jedno testovanie (to je v prípade, že hľadaný prvok je prostredným prvkom poľa) O(1). V najhoršom prípade je potrebné vykonať nasledovný počet testovaní: O( log2(N) ).
Binárne vyhľadávanie funguje len na zoradených poliach!
