Náplň prednášky:
- Aktualizácia
- Vzorkovanie signálu
- Rekonštrukcia signálu
- Praktické ukážky
| View file | ||||
|---|---|---|---|---|
|
Rekonštrukcia - Shannon-Kotelnikov rad
- Pri vzorkovacej teoréme bolo uvedené, že každý časový priebeh signálu, ktorý má ohraničené spektrum je jednoznačne určený postupnosťou svojich vzoriek odoberaných v rovnomerných časových intervaloch Td.
- V priestore ortogonálnych harmonických funkcii je pôvodný spojitý signál možné z jeho vzorkovanej podoby obnoviť (rekonštruovať) pomocou Shannonovho-Kotelnikového radu.
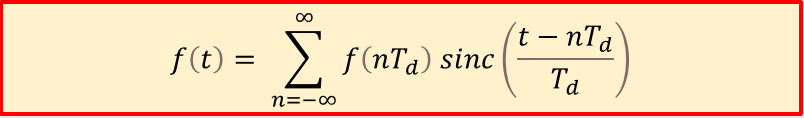
- Tento vzťah vo svojej podstate predstavuje sumu násobkov vzoriek a funkcie sinc(t), ktorá je posunutá do časového okamihu, v ktorom daná vzorka bola zo signálu získaná (nTd). Hodnota vzorky určuje maximálnu hodnotu danej funkcie sinc(t). Funkcia sin() nadobúda v časových okamihoch ostatných vzoriek nulovú hodnotu a nenulovú hodnotu inde. Je spojitá a teda výsledný signál je výsledkom súčtu všetkých takto posunutých funkcii.
Tiež vieme, že Fourierovátransformácia sinc funkcie je pravouhlý impulz.Teda pre rekonštrukciu signálu postačí diskrétny signál filtrovať ideálnym DP filtrom.
Odporúčané videa:
| Widget Connector | ||
|---|---|---|
|
| Widget Connector | ||
|---|---|---|
|